Решение задачи ежемесячного планирования закупок
при заданных cпросе, предложении, ценах, затратах на хранение методом динамического программирования.


p[i]  - отпускные цены в i-м месяце (₽/шт.)
q[i]  – закупочные цены в i-м месяце (₽/шт.)
b[i]  - спрос в i-м месяце          (шт.)
r[i]  – затраты на хранение единицы товара в i-м месяце (₽/шт.)
s[i]  – остаток на складе на конец i-го месяца
m  – вместимость склада


i ∈ {0,1,2,3,4,5,6,7,8,9,10,11}   (0, ... , n-1)

s[0] = s[n-1] = 0.

Найти 
a[i]  - закупки в i-м месяце 
------------------------------

h[i]  – прибыль за месяц i.
R[i]  – затраты на хранение за месяц i.

h[i] = b[i]*p[i] - a[i]*q[i] - R[i].

R[i] = r[i] * (s[i-1] + s[i]) / 2 .


  
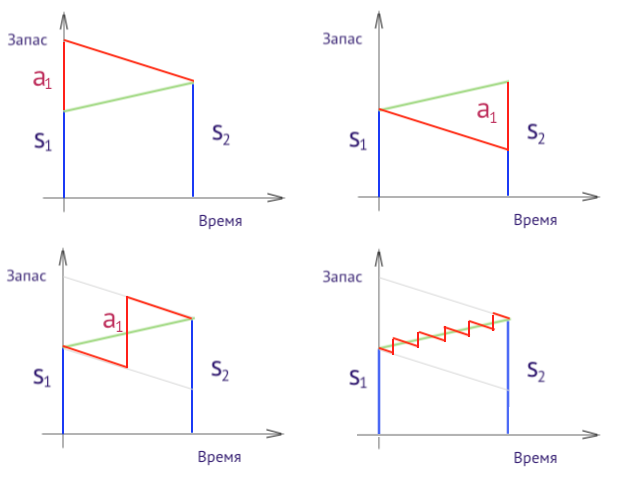
Затраты на хранение зависят от того, когда делались закупки.
Из рисунков видно, что при закупках в конце месяца затраты на хранение будут меньше.
При закупках в начале месяца затраты будут r1*(s1+a1+s2)/2, а при закупках
в конце месяца – r1*(s1+s2-a1)/2. Примем, что закупки делаются в середине месяца или
равномерно, тогда затраты на хранение в течение месяца будут иметь среднее значение r1*(s1+s2)/2

В начале года считается, что запасы на складе равны нулю.

Значения H(s[n-1]) вычисляются с заданной дискретностью и заносятся в таблицу.

Пусть расчёт по двум месяцам, тогда вычисляется таблица прибыли за первый месяц,
в зависимости от остатка в конце, а затем берётся такое значение остатка в конце 
первого месяца, при котором суммарная прибыль за два месяца оказывается наибольшей.

Если месяцев больше двух, то после вычисления таблицы прибыли за последний месяц,
будет вычислена таблица прибыли за предпоследний месяц. При этом, прибыль за 
предпоследний месяц зависит от двух параметров: остатка на начало предпоследнего
месяца и остатка на его конец H(s[n-2],s[n-1]). 
Для каждого параметра [n-2] нужно найти такой параметр s[n-1], чтобы сумма прибылей
за два последних месяца была наибольшей max(s[n-1]){H(s[n-2],s[n-1]) + H(s[n-1])}
Таким образом, можно создать одномерную таблицу наибольшей прибыли за последние два
месяца H[n-1](s[n-2]), зависящей от остатка товара на складе на начало предпоследнего
месяца. Зная таблицу прибыли H за два последних месяца можно составить такую же
таблицу за три последних месяца по тому же алгоритму.

И так дальше для всех предшествующих месяцев вплоть до первого, когда станут 
известны остатки s[i] для всех i, дающие наибольшую прибыль за все месяцы.
 
=======================================================
Формализация алгоритма.

Прибыль за последний месяц
H[n-1] = h[n-1] = b[n-1]*p[n-1] - a[n-1]*q[n-1] - (s[n-2] + 0) /2.

Прибыль за предпоследний месяц

h[n-2] = b[n-2]*p[n-2] - a[n-2]*q[n-2] - (s[n-3] + s[n-2]) /2.

H[n-2](s[n-3]) = max{s[n-2]}(h[n-2](s[n-3], s[n-2]) + H[n-1](s[n-2]))

H[i](s[i], s[i-1]) = 


Массивы создаваемые.

H от 0 до m,  

s от 0 до n-1,  s – остаток на конец месяца.

h от 0 до m, от 0 до m,   - прибыль текущего месяца от остатков на начало и конец месяца



Массивы начальных данных.
p[i] от 0 до n-1  - отпускные цены в i-м месяце (₽/шт.)
q[i] от 0 до n-1 – закупочные цены в i-м месяце (₽/шт.)
b[i] от 0 до n-1 - спрос в i-м месяце          (шт.)
r[i] от 0 до n-1 – затраты на хранение единицы товара в i-м месяце (₽/шт.)


Вычисляем таблицу прибыли за последний месяц

цикл по k от 0 до m 
        H[k] = b[n-1]*p[n-1] - a[n-1]*q[n-1] - (s[n-2] + 0)/2;

цикл по i от n-2 до 0  //по месяцам от предпоследнего до начального
  цикл по k от 0 до m 
    цикл по j от 0 до m 
      h[k][j] = b[i]*p[i] - a[i]*q[i] - (k + j) / 2;
  
  временный массив Ht от 0 до m 
  цикл по k от 0 до m   // для остатка k ищем наилучшую прибыль за этот и остальные месяцы
    Ht[k] = 0 
    цикл по j от 0 до m       
       если (h[k][j] + H[j]) > Ht[k] 
       то  Ht[k] = (h[k][j] + H[j]) //сохранение наибольшей прибыли за этот и остальные месяцы 
           s[i][k] = j;             //сохранение наилучшего остатка на конец месяца для остатка на начало

  H = Ht;      //Перенос данных из временного массива в основной

После завершения цикла по месяцам будет получен массив s для каждого месяца наилучших остатков.
Положив для начально месяца остаток на складе равный 0, возьмём из массива s наилучший для него 
остаток на конец месяца. По этому остатку из того же массива найдём наилучший остаток на следующий месяц.
Таким образом, получим оптимальную траекторию на пространстве месяцных остатков.
Зная спрос и остатки на каждый месяц найдём ежемесячные закупки.
        
Замечание.  Вычисление Ht[k] и h[k][j] можно объединить в один цикл.
В этом случае будет достаточно одиночной переменной h вместо двумерного массива, 
поскольку не потребуется сохранение прибыли за текущий месяц при разных значениях 
остатков на начало и конец месяца.