Задача о торговле сохраняемого продукта при случайном спросе  
Формула прибыли

    H  =  -q * (x - (x - a) / 2 * (x - a) / (b - a))  +
                + (p * (a + x) / 2 - r) * (x - a) / (b - a) +
                + p * x * (b - x) / (b - a);

После дифференцирования и приравнивания к нулю производной получается наилучший дневной запас                
x = b - r/(p-q).

Если запас меньше минимального спроса, то формула прибыли будет выглядеть по-другому.

H = x(p-q), то есть линейно убывает с убыванием x и в нуле обращается в нуль.
Отрицательный запас в этой задаче смысла не имеет.

Если запас больше наибольшего спроса, то каждый раз удовлетворяется весь спрос
и запас пополняется до спроса. Затраты на хранение каждый раз одинаковы.

H = y(p-q) - r = (p-q)(a+b)/2 - r. То есть, прибыль является постоянной величиной.

Компьютерная модель этой задачи представлена в java-классе RandomDemandStore
        

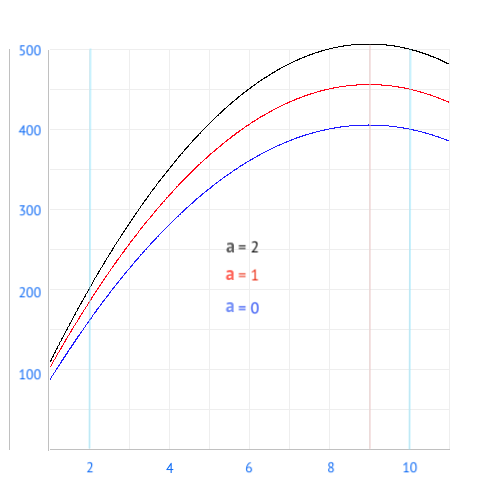
На рисунке показана зависимость прибыли 
от дневного запаса при разных левых границах 
a = 0,  a = 1  и  a = 2, где
p = 500,  q = 300,  r = 100, b = 10.
        

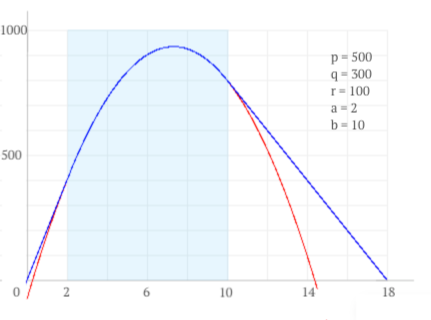
На рисунке изображена зависмость прибыли от спроса.
Если производная функции прибыли обращается в 0 за пределами изменения спроса,
то наибольшая прибыль будет при размере заказа, равном наименьшему спросу.
Корень производной не может быть больше наибольшего спроса, если закупочная
цена не меньше отпускной.        
        
===========================================================

Пусть в этой задаче затраты на хранение зависят от объёма сохраняемого товара.


  a – наименьший спрос
  b – наибольший спрос
  x - дневной запас
  z – остаток от предыдущего дня

  Стоимость дневного заказа – q(x - z) 
  
  
  При спросе меньше заказа  y < x  дневная выручка равна  py - rz.

  При спросе больше заказа  y ≥ x  дневная выручка равна  px.

  (b - x) / (b - a) – вероятность избыточного спроса.
  (x - a) / (b - a) – вероятность малого спроса.

  y = (a + x) / 2 – средний малый спрос.

  Средний остаток от предыдущего дня при малом спросе:
  z = x - y  =  x - a/2 - x/2  =  (x-a)/2.


       H =   -q * (x - (x - a) / 2 * (x - a) / (b - a))  +
                + (p * (a + x) / 2 - r * (x-a)/2) * (x - a) / (b - a) +
                + p * x * (b - x) / (b - a);

Первое слагаемое  -q * (x - (x - a) / 2 * (x - a) / (b - a)) =
               =  -q * (x(b - a) - (x - a) / 2 * (x - a)) / (b - a);
   без /(b-a)     -q * (x(b - a) - (x - a) / 2 * (x - a)) = -q * (bx - ax - (xx - 2ax + aa)/2 ) =
               =  -q * (bx - xx/2 - aa/2)  =
               =  -bqx + qxx/2 + qaa/2;

Второе слагаемое  (p * (x + a) / 2 - r*(x-a)/2) * (x - a) = (p * (x + a)(x - a) / 2 - r(x - a)(x - a)/2);
 без /(b-a)        pxx/2 - paa/2 - rxx/2 - raa/2 + rax ;

Третье слагаемое  p * x * (b - x) =
 без /(b-a)    =  pbx - pxx


H*(b-a) = -bqx + qxx/2 + qaa/2 + pxx/2 - paa/2 - rxx/2 - raa/2 + rax + pbx - pxx;

dH*(b-a)/dx  =  -bq + qx   +   px - rx + ra   +   pb - 2px  =   -bq + qx - px - r(x-a) + pb  =  -(p-q)x + b(p-q) - r(x-a)  = 
= -(p-q+r)x + b(p-q) + ra  = 0;

  x = (b(p-q) + ra) / (p-q+r)  ––– наилучший дневной запас


----------------------------------------
Когда запас меньше наименьшего спроса, то 
распродаётся весь дневной запас без остатка
и формула прибыли не отличается от предыдущего случая

H = x(p-q).     

Это линейная функция, прохдящая через точку (0,0).

В точке x=a совпадает со значением из квадратичной формулы прибыли.

----------------------------------------
Когда запас больше наибольшего спроса

Средний спрос y = (a+b)/2

Средний остаток z = x-y = x - (a+b)/2

Затраты на закупку (x-z)*q = (x - x + (a+b)/2)q = q(a+b)/2

Затраты на хранение rz = r(x - (a+b)/2)

Выручка py = p(a+b)/2

Прибыль  H = p(a+b)/2 - q(a+b)/2 - r(x - (a+b)/2) =  (p-q)(a+b)/2 - rx + r(a+b)/2 =

           = (p-q+r)(a+b)/2 - rx;

Это тоже линейная убывающая функция. При x = (p-q+r)(a+b)/(2r) равна нулю.
При x=b совпадает со значением квадратичной функции прибыли.