Задача о случайном спросе (непрерывный случай)
    
a – наименьший спрос
b – наибольший спрос
х – наивыгоднейший заказ
y – спрос

q – закупочная цена
p – отпускная цена

|------|====|
a      x    b

(x-a) – спрос меньше заказа
(b-x) – спрос больше заказа

Hs – прибыль для малого спроса
Hl – прибыль для избыточного спроса
H – ожидаемая прибыль

Нs = (-qx + py); вероятность Ps = (x-a)/(b-a),  y<x;

Hl = (-qx + px); вероятность Pl = (b-x)/(b-a),  y>x;

H = Hs*Ps + Hl*Pl = (py - qx)*(x-a)/(b-a) + (px - qx)*(b-x)/(b-a);

(x+a)/2 – средний спрос меньше заказа

H = (p*(x+a)/2 - qx)*(x-a)/(b-a) + (px - qx)*(b-x)/(b-a) = 

    (x*(p/2-q) + pa/2) * (x-a)/(b-a)  +  x*(p-q)*(b-x)/(b-a);


H'(x) = (p/2-q) * (x-a)/(b-a) + (x*(p/2-q) + pa/2)/(b-a)  +  (b-2x)*(p-q)/(b-a);

(p/2-q) * (x-a) + (x*(p/2-q) + pa/2)  +  (b-2x)*(p-q) = 0;

x*(p/2-q + p/2-q + 2(q-p)) + (p/2-q)*(-a) + pa/2 + b*(p-q) = 0;

x*(p/2 - q + p/2 - q + 2q-2p) - ap/2 + aq + pa/2 + bp - bq = 0;

x*(-p)  + aq + bp-bq = 0;  

-x*p + aq - paa/2 + bp-bq = 0;  

        aq + bp - bq                
x =  ––––––––––––––––––––––––– = a * q/p + b - b * q/p  =  a(q/p) + b(1 - q/p).    b(1-t) + at.
             p                      


4 * (1 - 30/50) = 4 * 2/5 = 1.6 .



  =========================================

     Дискретный случай


a – наименьший спрос
b – наибольший спрос
х – наивыгоднейший заказ
y – спрос

q – закупочная цена
p – отпускная цена

   1234567890
   ------====
   a     x  b


(x-a)   – спрос меньше заказа
(b-x+1) – спрос больше или равен заказу

Hs – прибыль для малого спроса
Hl – прибыль для избыточного спроса
H – ожидаемая прибыль

Нs = (-qx + py); вероятность Ps = (x-a)/(b-a+1),  y<x;

Hl = (-qx + px); вероятность Pl = (b-x+1)/(b-a+1),  y>x;

H = Hs*Ps + Hl*Pl = (py - qx)*(x-a)/(b-a+1) + (px - qx)*(b-x+1)/(b-a+1);

(a+x-1)/2 – средний спрос меньше заказа

...

================================================

 Непрерывный случай для произвольного распределния



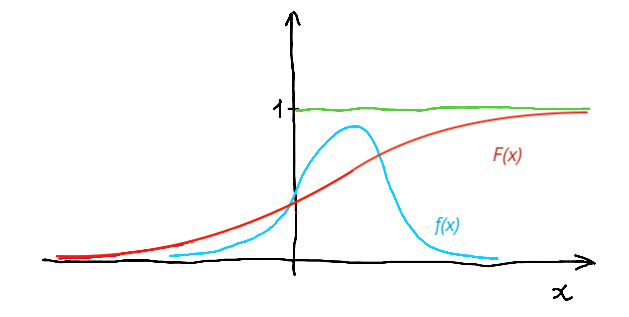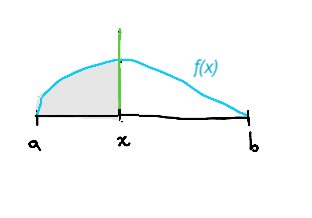
f(x) – плотность
F(x) – интеграл плотности