Обобщение формулы Уилсона

λ – скорость пополнения запаса
ν – скорость расходования запаса
Y – наибольший запас на складе
y – наибольший (по модулю) дефицит
q – размер поставки
τ – время между поставками
K – расходы по доставке партии товара
s – удельные расходы хранения
d – удельные расходы дефицита

τ1 – время пополнения запасов от 0 до Y
τ2 – время расходования запасов до нуля
τ3 – время накопления дефицита
τ4 – время восполнения дефицита
  
τ1 + τ2 + τ3 + τ4 = τ 




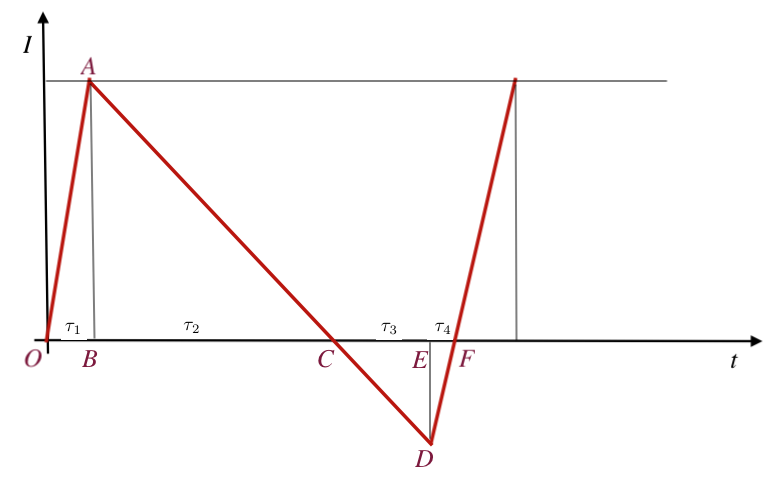Y = AB = τ1*(λ-ν) = τ2*ν
y = ED = τ3*ν = τ4*(λ-ν) 

τ1 = τ2*ν/(λ-ν), τ4 = τ3*ν/(λ-ν), 

τ = λ*(τ2+τ3)/(λ-ν)

Ls – расходы на хранение запасов за время τ1+τ2.

Ls = 0.5 * s*Y*(τ1 + τ2) = s*τ2*ν*(τ2*ν/(λ-ν)+τ2) = (s*λ*ν*(τ2)^2)/(λ-ν)

Ld – расходы на обслуживание дефицита за время τ3+τ4.

Ld = 0.5 * d*y*(τ3 + τ4) = (d*λ*ν*(τ3)^2)/(λ-ν)

L = Ls + Ld + K  –  суммарные издержки за время τ (один цикл)

L = K + (λ*ν)/(λ-ν) * (s*(τ2)^2 + d*(τ3)^2).


           K*(λ-ν) + 0.5*λ*ν*(s*(τ2)^2 + d*(τ3)^2) 
H = L/τ = ––––––––––––––––––––––––––––––––––––––––– 
                        λ*(τ2+τ3)

Частные производные H по τ2 и τ3 приравниваются к 0 и решается система уравнений.



Откуда

τ2 = sqrt((2*K)/(s*ν)) * sqrt((1-ν/λ)/(1+s/d)); 

τ3 = (s/d)*τ2 = (s/d) * sqrt((2*K)/(s*ν)) * sqrt((1-ν/λ)/(1+s/d)); 

τ1 = (1/λ) * sqrt((2*K*ν)/s) * 1/sqrt((1-ν/λ)*(1+s/d));

τ4 = (s/d)*τ1 = (s/d) * (1/λ) * sqrt((2*K*ν)/s) * 1/sqrt((1-ν/λ)*(1+s/d));

τ = sqrt((2*K)/(s*ν)) * sqrt((1+s/d)/(1-ν/λ));

q = sqrt((2*K*ν)/s) * sqrt((1+s/d)/(1-ν/λ));

H = sqrt(2*K*ν*s) * sqrt((1-ν/λ)/(1+s/d)); 

Y = sqrt((2*K*ν)/s) * sqrt((1-ν/λ)/(1+s/d));

y =  = (s/d)*Y = (s/d) * sqrt((2*K*ν)/s) * sqrt((1-ν/λ)/(1+s/d));